Photonic multitasking enabled with geometric phase
The constructive and destructive interference of waves is often exploited in optics and signal transmission. The interference pattern is a direct measure of the phase difference between two or more beams. Such a phase difference may result from the difference between the optical paths traversed by the light beams. However, phase can change for a single beam if it propagates through an “anisotropic parameter space,” a medium that curves the light; this property is called geometric or topological phase (1–4). On page 1202 of this issue, Maguid et al. (5) use
“Modern photonics applications, however, call for ultracompact, multifunctional, integrated optical devices…”
metasurfaces—ultrathin, planar engineered structures (6–9)—to form shared-aperture antenna arrays that impart geometric phase to optical signals. These devices can control photonic spin and enable multiple optical functions.
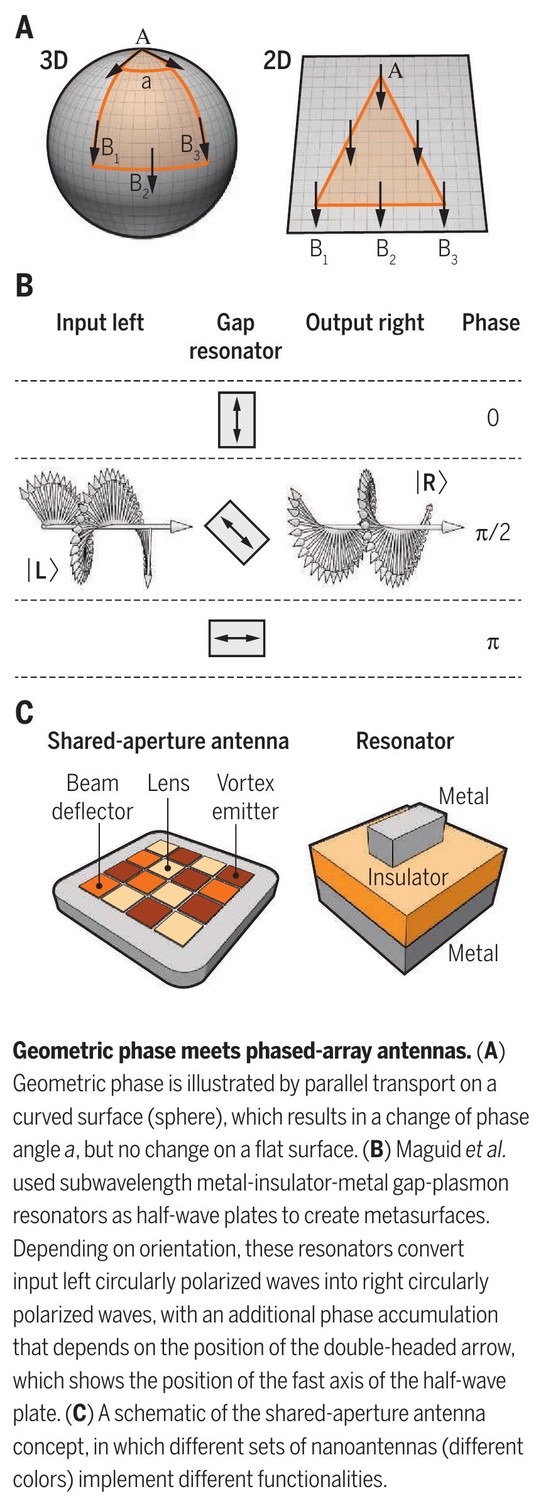
Geometric phase shift arises when rotations are caused by moving through an anisotropic parameter space, so the phase will depend on the path traveled. Consider moving an arrow over a sphere, with the requirement that it always stays in the plane tangent to the surface of the sphere; the arrow can be thought of as the top of a wavefront (see the figure, panel A). If we move the arrow without rotating it around the axis normal to the surface, after completion of the closed path, it rotates by an angle α. Had we traveled twice as far along the bottom arc, the angle would have been 2α. Thus, the angle depends on the paths taken to return to the top. On a flat surface, the arrow would have remained parallel to its original orientation throughout the circuit.
This difference in so-called parallel transport on a curved or flat surface is a direct result of the geometric phase. One of the manifestations of the geometric phase in optics is the Pancharatnam-Berry phase that appears when the polarization of a light beam evolves along a similar geodesic triangle, but on the Poincaré sphere commonly used to describe these phase relations (10), the phases of the final and initial states differ by an amount equal to half of the solid angle enclosed by the triangle.
Unlike conventional optical components such as lenses or prisms that introduce phase changes through optical path differences, metasurfaces facilitate strong light-matter interaction on a subwavelength scale through the careful arrangement of resonant optical antennas.
Phase accumulation in gradient metasurfaces results from space-variant polarization manipulations, as opposed to requiring propagation through a certain thickness of a material to accumulate sufficient phase. A variety of gradient metasurfaces, where antennas with subwavelength separation and spatially varyingshape, size, and orientation enable optical wavefront shaping, have been demonstrated. These types of structure have enabled a plethora of potential functionalities, including beam steering, lensing, holography, and structured light generation (11).
Building further on this approach, Maguid et al. created complex geometric-phase metasurfaces from subwavelength half-wave-plate elements. These wave plates are the metal-insulator-metal structures, with the top metal layer consisting of a periodic arrangement of nanoantennas forming from gap-plasmon resonators (see the figure, panel B) (12). Like the birefringent mineral calcite, these structures introduce different phase shift in different directions. The main difference, however, is that in conventional macroscopic wave plates, such differential phase shifts are introduced by the direction-dependent difference in refractive indices, whereas in metasurfaces, they rely on the two electric dipole scatterers whose resonances are oppositely detuned from a design frequency. The wave plates are oriented so that one of these directions, the fast axis, depends on the spatial position. By manipulating the local orientations of the nanoantennas, multiple wave fronts with different functionalities are generated. The resulting polarization is space-varying because it depends on the local orientation of the wave plate. Thus, at different points, the beam navigates different paths on the Poincaré sphere, resulting in a space-variant phase-front modification originating from the geometric phase.
A majority of the metasurfaces that have been reported were designed to enable a single functionality. Modern photonics applications, however, call for ultracompact, multifunctional, integrated optical devices that enable independent control of the phase, amplitude, and polarization. Building on the concept of shared-aperture antennas (13), which are a class of phased-array antennas originally introduced to steer radar beams, Maguid et al. address this critical need and demonstrate multifunctional, geometric-phase metasurfaces. The antennas use a single common aperture to perform multiple functions simultaneously (see the figure, panel C).
Several individual functionalities can be combined on the same platform in three different ways: segmentation, interleaving, and harmonic response. Geometric-phase metasurfaces with interleaved and asymmetric harmonic response are excellent candidates for realizing on-demand, multifunctional on-chip photonics. As an example, Maguid et al. converted a conventional linearly polarized beam into azimuthally and radially polarized beams that carry orbital angular momentum. Moreover, space-variant polarization manipulation enables the realization of multiple vectorial optical vortices by the coherent superposition of wavefronts with opposite helicities. Such complex beams are of interest for the next generation of optical communication systems, as they offer the opportunity to facilitate an entirely new technology for increasing future optical network capacity.
Finally, Maguid et al. used interleaved geometric-phase metasurfaces to build a simple and ultracompact spectropolarimeter. This device simultaneously measures the polarization state and spectrum of a wave transmitted through a semitransparent object. Potential applications include drug development, cancer diagnostics, remote sensing, and astrophysics. The alliance between the geometric phase and the shared-aperture antenna arrays technology enables multifunctional wavefront shaping using a single, achromatic, and ultrathin nanoscale broadband photonic device.
References
1. M. V. Berry, Sci. Am. 259, 46 (June 1988).
2. S. Pancharatnam, Proc. Ind. Acad. Sci. 44, 247 (1956).
3. M. V. Berry, J. Mod. Opt. 34, 1401 (1987).
4. N. Herbert, New Scientist 1564, 37 (1987).
5. E. Maguid et al., Science 352, 1202 (2016).
6. D. Lin, P. Fan, E. Hasman, M. L. Brongersma, Science 345, 298 (2014).
7. N. Yu et al., Science 334, 333 (2011).
8. X. Yin, Z. Ye, J. Rho, Y. Wang, X. Zhang, Science 339, 1405 (2013).
9. M. I. Shalaev et al., Nano Lett. 15, 6261 (2015).
10. Z. Bomzon, V. Kleiner, E. Hasman, Opt. Lett. 26, 1424 (2001).
11. N. Yu, F. Capasso, J. Lightwave Technol. 33, 2344 (2015).
12. A. Pors, M. G. Nielsen, S. I. Bozhevolnyi, Opt. Lett. 38, 513 (2013).
13. R. L. Haupt, IEEE Trans. Antennas Propag. 53, 2858 (2005)