§ 4.1. Теоретический материал
Диэлектрики – это материальные тела, в которых нет свободных зарядов, способных под действием электрического поля перемещаться на большие, макроскопические расстояния (в отличие от проводников). Заряды в диэлектрике могут перемещаться под действием внешнего электрического поля на расстояния порядка атомных.
Электрическое поле в диэлектрике. При действии внешнего электрического поля положительные и отрицательные заряды в диэлектрике смещаются в пределах молекулы в противоположных направлениях. Такая система сама порождает электрическое поле. Поле в произвольной точке пространства становится суммой внешнего поля и поля, созданного системой разделенных зарядов диэлектрика.
Дипольный момент. В первом приближении электрические свойства нейтральной системы с неоднородным распределением плотности заряда характеризуются ее дипольным моментом:
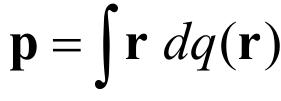
Значение дипольного момента электрически нейтральной системы не зависит от выбора начала системы отсчета. Поэтому радиус-вектор r можно отсчитывать от любой точки, выбранной за начало координат. На больших расстояниях от системы ее электрическое поле совпадает с полем точечного диполя (гл. 1, формула (1.4)).
Поляризация. Процесс образования (или упорядочения) дипольных моментов внутри диэлектрика называется поляризацией. Поляризация может происходить за счет смещения зарядов в атомах и молекулах диэлектрика при действии внешнего поля, за счет упорядочения ориентации дипольных моментов атомов с несимметричным распределением внутриатомного заряда и по ряду других причин. Разделенные в процессе поляризации заряды называются поляризационными (или связанными) зарядами. Связанные заряды могут быть как объемными, так и поверхностными. Гл.4. Диэлектрики в электростатическом поле 111 Заряды в диэлектрике, не входящие в состав его атомов и молекул, называются сторонними зарядами (иногда их условно называют свободными зарядами, хотя в ряде случаев сторонние заряды могут быть и не свободными).
Поляризованность (вектор поляризации) P диэлектрика – это вектор объемной плотности дипольного момента. Численно он равен дипольному моменту единицы объема диэлектрика:
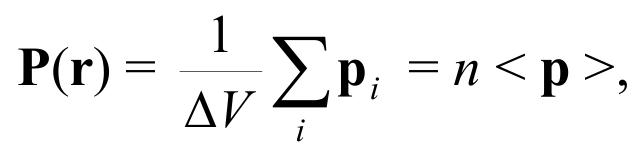
где ∆V – физически бесконечно малый объем диэлектрика в окрестности точки с радиус-вектором r, pi – дипольный момент i-той молекулы из этого объема, n – концентрация молекул в диэлектрике, < p > – среднее значение pi в объеме ∆V.
Плотность объемных связанных зарядов в поляризованном диэлектрике равна
ρ′ = – div P. (4.1)
Она отлична от нуля только в случае неоднородной поляризации. Ниже все связанные (поляризационные) заряды будут обозначаться штрихом (в учебниках встречаются также обозначения индексами "пол" или "св").
Плотность поверхностных связанных зарядов σ′ на границе раздела двух диэлектриков равна
σ′ = – n12 (P2 – P1) = P1n – P2n, (4.2)
где n12 – единичный вектор нормали, направленный из первой среды во вторую. Нормальная компонента вектора P испытывает на границе раздела диэлектриков скачок, равный плотности связанного заряда.
Теорема Гаусса для вектора поляризации:
dq
S
PS∫ = −′ , (4.3)
где q′ – полный связанный заряд, находящийся внутри замкнутой
поверхности S.
Напряженность электрического поля в диэлектрике – это
сумма напряженности Е0 поля сторонних зарядов в данной точке в
отсутствие диэлектрика и напряженности Е′ от всех связанных за-
рядов, возникших в результате поляризации диэлектрика:
211ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
Е = Е0 + Е′.
Если поляризация вызвана сторонними зарядами, то поле индуци-
рованных связанных зарядов направлено так, что всегда уменьшает
напряженность поля сторонних зарядов, т.е. Е < Е0. Поэтому это
поле часто называют деполяризующим полем.
Диэлектрическая восприимчивость. Во многих случаях по-
ляризованность P диэлектрика пропорциональна напряженности
поля в диэлектрике E, а свойства диэлектрика по всем направлени-
ям можно считать одинаковыми (такой диэлектрик называется ли-
нейным изотропным). Для такого диэлектрика
P = ж ε0E, (4.4)
где коэффициент ж называется диэлектрической восприимчиво-
стью. Это соотношение неприменимо к диэлектрикам с постоянной
поляризованностью (например, к электретам), когда вектор Р опре-
деляется не внешним полем, а внутренними структурными факто-
рами. В общем случае, который мы рассматривать не будем, связь
векторов P и E тензорная и при больших величинах Е – нелиней-
ная.
Если внутри однородного и изотропного диэлектрического
тела отсутствуют сторонние заряды, то при воздействии на него
произвольного электростатического поля в нем возникают только
поверхностные связанные заряды σ′ ≠ 0, а плотность объемных свя-
занных зарядов в любой точке равна нулю ρ′ = 0.
Вектор электрического смещения или вектор электриче-
ской индукции (оба названия эквивалентны) определяется соот-
ношением
D = ε0E + P. (4.5)
Если выполняется (4.4), то векторы D и Е связаны линейно:
D = εε0E. (4.6)
Величина
ε = (1 + ж) (4.7)
называется относительной диэлектрической проницаемостью (час-
то ее сокращенно называют проницаемостью диэлектрика).
Вектор D не является чисто полевым вектором, так как он учи-
тывает поляризованность среды. Он является суммой двух совер-
шенно различных по физическому смыслу слагаемых и поэтому не
имеет глубокого физического смысла. Однако в математическом
отношении использование векторного поля D в ряде случаев упро-
Гл.4. Диэлектрики в электростатическом поле 113
щает расчеты электростатических полей в диэлектриках. Это свя-
зано с тем обстоятельством, что в определении вектора D учтен
вклад в электрическое поле от связанных зарядов. В однородных
изотропных диэлектриках с линейной восприимчивостью, т.е. под-
чиняющихся соотношению (4.6), источниками векторного поля D
являются только сторонние заряды, поэтому в этом случае при на-
хождении поля D можно как бы "забыть" о существовании связан-
ных зарядов.
Для вектора D имеет место дифференциальное соотношение
div D = ρ, (4.8)
где ρ – плотность сторонних зарядов.
Свойства вектора электрического смещения. В диэлектри-
ках, подчиняющихся (4.6), векторное поле D(r) потенциально и
аналогично по свойствам электростатическому полю напряженно-
сти E(r). Это означает, что rot D = 0, а линии поля D начинаются и
заканчиваются на сторонних зарядах (или в бесконечности), а в
точках без сторонних зарядов они непрерывны (включая и точки, в
которых находятся связанные заряды). Поэтому для нахождения
поля D можно использовать все формулы, относящиеся к расчету
напряженности электрического поля E в вакууме, только подстав-
лять в них нужно уже не все заряды, а только сторонние заряды, и
убрать из этих формул множитель ε0.
Если же соотношение (4.6) в диэлектрике не выполняется, поле
D может иметь вихревую компоненту, у которой линии D замкну-
ты и для возникновения которой не требуются свободные заряды.
Например, такова ситуация в электретах, т.е. диэлектриках с посто-
янной поляризованностью, рассмотренных ниже (задача 4.3.14).
Интегральная электростатическая теорема Гаусса для век-
тора D:
∫
S
Dd S = q, (4.9)
где q – полный сторонний заряд, находящийся внутри замкнутой
поверхности S. Теорема справедлива при любом расположении
произвольной поверхности S относительно диэлектрических тел.
Если однородным диэлектриком заполнить весь объем между лю-
быми эквипотенциальными поверхностями поля, существовавшего
в отсутствие диэлектрика, то напряженность поля в диэлектрике
будет в ε раз меньше, чем она была в соответствующей точке до
введения диэлектрика. В частности, для точечного заряда в безгра-
411ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
ничной однородной диэлектрической среде с проницаемостью ε
электрическое смещение и напряженность электрического поля
будут равны
2
4
1
()
r
q
Dr
π
= и 2
0
4
1
()
r
q
Er
επε
= . (4.10)
Если все пространство между обкладками плоского, цилинд-
рического или сферического конденсатора заполнить однородным
изотропным диэлектриком, то напряженность поля в диэлектрике
будет в ε раз меньше, чем напряженность поля в точно таком же
конденсаторе до заполнения его диэлектриком, а соответственно,
емкости конденсаторов будут в ε раз больше.
Граничные условия. На границе раздела двух диэлектриков 1
и 2:
E2t = E1t , (4.11)
D2n –D1n = σ, (4.12)
где σ – плотность сторонних зарядов на границе раздела, а вектор
нормали n направлен из первой среды во вторую.
Если на границе раздела двух диэлектриков отсутствуют сторонние
заряды, то нормальная компонента вектора D непрерывна при пе-
реходе через границу
D2n = D1n (4.13)
Для такого случая выражение для плотности связанных поверхно-
стных зарядов на границе (4.2) можно записать как
σ′ = ε0(E2n – E1n) (4.14)
Если ε2 > ε1 и поле направлено из первой среды во вторую, то σ′ < 0.
Если ε2 > ε1 и поле направлено из второй среды в первую, то σ′ > 0.
В том и другом случае поле во второй среде (с большей ε) слабее,
чем в первой (где ε меньше). При ε1 > ε2 знаки связанных зарядов
надо заменить на противоположные (см. [1] §17).